1 加权残差法和伽辽金近似
1.1 经典问题引入
考虑确定一根长度为\(L\)、横截面恒定的细长均质金属杆的热传导情况。假定左端暴露在规定的热通量\(q\)下,右端保持恒温\(T=T_L\),并且棒的长度方向被绝缘材料包围。利用傅立叶定律,我们可以写出控制整个棒的温度分布的导线方程,即:
\[-K\frac{d^2T}{dx^2}=Q,0<x<L\tag{1.1}\]
式中
\(x\)为长度坐标
\(K\)是材料的热传导率(假定为常数)
\(Q\)是单位体积产生的热量
与这一问题相应的边界条件是 \[-K\frac{dT}{dx}=q,x=0\tag{1.2}\] \[T=T_L,x=L\tag{1.3}\] 当\(q>0\)时,热量流向\(x=0\)处的棒体,这就是公式(1.2)中负号的原因。
假定\(Q\)是可积的,那么方程(1.1)的解与边界条件(1.2)和(1.3)可以通过直接积分求得: \[T(x)=T_L+\frac{q}{K}(L-x)+\frac{1}{K}\int^L_x(\int^x_0Q(z)dz)dy\tag{1.4}\] 如果\(Q\)为常数,公式(1.4)简化为: \[T(x)=T_L+\frac{q}{K}(L-x)+\frac{Q}{2K}(L^2-x^2)\tag{1.5}\]
1.2 弱形式描述
通常有两种方法可以用有限元来计算和求解方程(1.1)的形式,这两种方法分别称为Rayleigh-Ritz法和Galerkin法。其他较少使用的方法是基于配位、常数加权和最小平方技术。所有求解方法都属于加权残差法。
无论我们使用哪种方法,第一步都是在\(0\le x
\le
L\)的区间内划分出网格,网格由一定数量的非重叠子区间组成,覆盖整个域,每个子区间称为一个
"单元"。我们用\(e_k\)表示每个单元,即\(e_k=\{x:x_k\le x\le
x_{k+1}\}\)。每个子区间的端点\(x_k\)称为节点。
温度分布由每个子区间的预设函数(用\(\phi_j(x)\)表示)和相应的未知参数\(a_j\)计算得到。
因此,我们将一个单元定义为一个子区间\(e_k\),以及一组预先确定的函数\(\varphi_j\)和相同数量的参数\(a_j\)。这样如果参数\(a_j\)已知,则温度长边的近似值\(T(x)\)也是已知的。在整个域\(0 \le x \le L\)上,我们可以写出 \[T(x)\cong
a_1\phi_1(x)+a_2\phi_2(x)+\cdots+a_{n+1}\phi_{n+1}(x)\tag{1.6}
\] 函数\(\phi(x)\)称作形状函数,我们将式(1.6)写成求和的形式,即
\[T(x)=\sum^{n+1}_{i=1}a_i\phi_i(x)\tag{1.7}
\]
Ritz方法从数学的角度更满足预期,可以让我们形成更近似和收敛的数理论,但是在解决流体和热传导问题时,显得捉襟见肘。
当使用 (1.7)
形式的表达式近似求解问题时,一般来说,我们无法得到这个偏微分方程的真实解。因此,如果我们将近似解替换为方程(1.1)的左侧,我们得到的将不是同一值,而是与误差相关的某个
"残差 "函数。我们将这个残余误差定义为 \[R(T,x)\equiv-K\frac{d^2T}{dx^2}-Q\tag{1.8}\]
这里,\(T\)是真实解\(T^*\)的近似解,即\(R(T^*,x)\equiv 0\)。然而,对任意的\(T\neq T^*\),我们不能令残差在每个\(x\)点都消失。加权残差法的原理是,我们可以将残差乘以加权函数,令加权残差的积分在每一点\(x\)上变为0,即 \[\int^L_0W(x)R(T,x)dx=0\tag{1.9}\]
式中\(W(x)\)为权重函数。通过选择不同的权重函数并将其替换到弱形式(1.9)中,我们可以生成一个关于未知参数\(a_j\)线性方程组,该方程组用于确定偏微分方程近似解\(T\)的形式,该近似解类似于方程(1.7)给出的有限级数。这种方法满足偏微分方程的“平均”或“积分”意义上的解。所选加权函数的类型取决于所选加权残差函数的类型。在Galerkin方法中,权重与形状函数\(\phi(x)\)相等,即\(W_i(x)=\phi_i(x)\)。
由于未知参数\(a_j\)的数量等于形状函数\(\phi_j\)的数量,将生成一个方程数量与未知数数量相同的线性代数方程组。如果与偏微分方程相关的边界条件被正确设定和施加,那么这样的方程组的存在性和唯一性是保证的。
我们现在希望使用我们提出的形状函数\(\phi(x)\)作为权重函数\(W(x)\)来评估方程(1.9)的左端积分。因此,根据伽辽金方法得到:
\[\int^L_0\phi(x)\Big
[-K\frac{d^2T}{dx^2}-Q\Big ]dx=0\tag{1.10}\]
我们需要找到方程(1.7)中函数\(\phi(x)\)的适当形式。由于温度分布必须是\(x\)的连续函数,最简单的方法是在每个单元上使用分段多项式插值来近似它;特别是,分段线性近似提供了最简单的连续函数近似。不幸的是,这样的函数的一阶导数在单元节点处不连续,因此,在这些地方不存在二阶导数;此外,\(T\)的二阶导数在每个单元内部将消失。然而,要求二阶导数在所有地方都存在是过于严格的。这将阻止我们处理许多非常有兴趣的物理情况,例如在杆中存在一个单位强度的热源。在这种情况下,方程(1.1)变为
\[-K\frac{d^2T}{dx^2}=\delta(x-x_s)\tag{1.11}\]
式中\(\delta\)为Delta函数,在\(x=x_s\)外的各点为0,且在这一点处的值不确定。显然,在\(x=x_s\)处\(T\)的二阶导数不存在;方程(1.11)的解为:
\[T(x)=
\begin{cases}
-\dfrac{1}{K}[q(x-L)+(x_s-L)]+T_L&0\le x\le x_s\\
-\dfrac{1}{K}q(x-L)(x-L)+T_L&x_s\le x\le L
\end{cases}\tag{1.12}
\] 对方程(1.10)应用分部积分,得到 \[\int^L_0\phi(x)\left[-K\frac{d^2
T}{dx^2}\right]dx=\int^L_0K\frac{d\phi}{dx}\frac{dT}{dx}dx-K\phi\frac{dT}{dx}\Big
|^L_0\tag{1.13}
\] 于是方程(1.10)可重写为 \[\int^L_0K\frac{d\phi}{dx}\frac{dT}{dx}dx-\int^L_0\phi
Qdx-K\phi\frac{dT}{dx}\Big |^L_0=0\tag{1.14}
\] 这仅仅是一个“弱”形式的问题,因为它只包含解\(T(x)\)的一阶导数,而方程(1.10)包含二阶导数。对函数\(T(x)\)的微分要求已经减弱,因此得名“弱形式”。请注意,到目前为止还没有进行任何近似,也就是说,在表述中没有丢失任何东西,另一方面,简单的分段线性近似现在变得合理。
对每个权重函数\(\phi(x)\)使用公式(1.7),可将方程(1.14)改写为 \[\sum^{n+1}_{j=1}K\Big [\int^L_0\frac{d\phi_i}{dx}\frac{d\phi_j}{dx}dx\Big ]a_j-\int^L_0\phi_iQdx+\phi_i\Big[-K\frac{dT}{dx}\Big]\Big |^{x=L}_{x=0}=0\\ i=1,2,\cdots,n+1\tag{1.16} \] 一旦形状函数\(\phi_i\)选择好后,可以计算上式的积分。弱形式的伽辽金描述的优势在于,只有有限数量的参数\(a_i\)需要确定,\(i = 1, \cdots, n + 1\),这与方程(1.1)或(1.9)中需要确定\(0 \le x < L\)区间内每个点的\(T(x)\)值不同。在这种情况下,考虑精确解被兼容的近似所取代。例1 考虑方程(1.1),使用边界条件\(T(0)=T_0\)以及对流边界条件\(-K\frac{dT}{dx}\Big |_{x=L}=h(T-T_\infty)\)。式中\(h\)为热对流传导常数,\(T_\infty\)为参考温度。 加权残差公式(式(1.9)),对于这个问题保持不变,因为它由式(1.1)推导而来,与给定的边界条件无关。令边界处的热流项为0,即\(\phi(0) = 0\),并使用对流边界条件,方程(1.9)的形式变为 \[\int^L_0K\frac{d\phi}{dx}\frac{dT}{dx}-\int^L_0\phi Qdx+\phi(L)h(T_L-T_\infty)=0\tag{1.15}\] 即加权残差公式。稍后,我们将进一步要求加权函数在边界点处等于1。在这种情况下,\(\phi(L) = 1\),因此加权函数永远不会明确出现在边界项中。
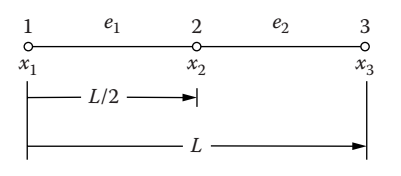
为了说明上述过程,我们将区间\([0, 1]\)分为两个等长的段,并在每个段的两个端点放置一个节点。因此,三个节点定义了整个杆的温度场,即节点\(1\)位于\(x = x_1 = 0\),节点\(2\)位于\(x = x_2 = L/2\),节点\(3\)位于\(x = x_3 = L\),如图1所示。
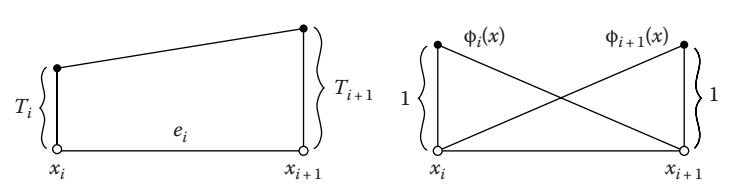
方程(1.17)~(1.19)可以使用矩阵形式表述为 \[T(x)=\phi \boldsymbol{a}\tag{1.20}\] 式中 \[\phi=\begin{matrix} [\phi_i &\phi_{i+1}] \end{matrix}\tag{1.21}\] 由此得到 \[\frac{dT}{dx}=\frac{d}{dx}\phi\boldsymbol{a}= \left[\begin{matrix} \dfrac{d\phi_i}{dx}&\dfrac{d\phi_{i+1}}{dx} \end{matrix} \right] \Big[ \begin{matrix} a_i\\a_{i+1} \end{matrix} \Big]\tag{1.22}\] 其中 \[\frac{d}{dx}\phi=\left[ \begin{matrix} -\dfrac{1}{x_{i+1}-x_i}&\dfrac{1}{x_{i+1}-x_i} \end{matrix} \right]\tag{1.23}\] 现在可将以上方程带入到方程(1.16)中,得到 \[\sum^2_{j=1}K\left[\int^{L/2}_0\frac{d\phi_1}{dx}\frac{d\phi_j}{dx}dx\right]a_j-\int^{L/2}_0\phi_1(x)Qdx-K\phi_1(x)\frac{dT}{dx}\Big|^{x=L/2}_{x=0}=0\\ \tag{1.24a}\] 和 \[\sum^2_{j=1}K\left[\int^{L/2}_0\frac{d\phi_2}{dx}\frac{d\phi_j}{dx}dx\right]a_j-\int^{L/2}_0\phi_2(x)Qdx-K\phi_2(x)\frac{dT}{dx}\Big|^{x=L/2}_{x=0}=0\\ \tag{1.24b}\] 上式使用方程(1.20)~(1.23)表述为 \[K\left[\int^{L/2}_0\left[\frac{d}{dx}\phi\right]^T\left[\frac{d}{dx}\phi\right]dx\right]\boldsymbol{a}-Q\int^{L/2}_0\phi^Tdx-\left[ \begin{matrix} q\\0 \end{matrix} \right]=0\tag{1.25}\] 代入 \[\phi=\left[ \begin{matrix} 1-\dfrac{2x}{L}&\dfrac{2x}{L} \end{matrix} \right]\] 和 \[\frac{d}{dx}\phi=\Big[ \begin{matrix} -\dfrac{2}{L}&\dfrac{2}{L} \end{matrix} \Big]\] 并积分,得到 \[\frac{2K}{L}\left[ \begin{matrix} 1&-1\\ -1&1\\ \end{matrix} \right] \left[ \begin{matrix} a_1\\ a_2 \end{matrix} \right]-\frac{QL}{4} \left[ \begin{matrix} 1\\1 \end{matrix} \right]- \Big[\begin{matrix} q\\0 \end{matrix} \Big]=\Big[\begin{matrix} 0\\0 \end{matrix} \Big]\tag{1.26}\] 单元\(2\)使用相似的方法计算得到 \[\frac{2K}{L}\Big[ \begin{matrix} 1&-1\\ -1&1\\ \end{matrix} \Big] \Big[ \begin{matrix} a_2\\ a_3 \end{matrix} \Big]-\frac{QL}{4} \Big[ \begin{matrix} 1\\1 \end{matrix} \Big]- \Big[\begin{matrix} q\\0 \end{matrix} \Big]=\Big[\begin{matrix} 0\\0 \end{matrix} \Big]\tag{1.27}\] 表达式(1.26)和(1.27)通过“组装”,即将方程(1.26)中的第二个方程和方程(1.27)中的第一个方程相加,因为它们都对应于相同的权重函数\(\phi_2(x)\),于是得到 \[\frac{2K}{L}\left[ \begin{matrix} 1&-1&0\\ -1&2&-1\\ 0&-1&1 \end{matrix} \right] \left[ \begin{matrix} a_1\\ a_2\\ a_3 \end{matrix} \right]= \left[ \begin{matrix} q\\ 0\\ 0 \end{matrix} \right]+\frac{QL}{4} \left[ \begin{matrix} 1\\ 2\\ 1 \end{matrix} \right]\tag{1.28} \] 由于已知\(a_3=T_L\),上述公式简化为关于未知数\(a_1\)和\(a_2\),即 \[a_1-a_2=\frac{ql}{2K}+\frac{QL^2}{8K}\tag{1.29a}\] \[-a_1+2a_2=\frac{QL^2}{4K}+T_L\tag{1.29b}\] 解为 \[a_1=\frac{qL}{K}+\frac{QL^2}{2K}+T_L,\\ a_2=\frac{qL}{2K}+\frac{3QL^2}{8K}+T_L,\\ a_3=T_L\tag{1.30}\]
1.3 小结
有限元方法的基本原理在于加权残差法。最常用的两种程序是Rayleigh-Ritz方法和伽辽金方法。Rayleigh-Ritz方法基于变分计算;然而,这种方法不能用于一些更复杂的方程。伽辽金方法简单易用,即使Rayleigh-Ritz方法无法应用,也能保证得到与主导微分方程兼容的近似解。 在这两种方法中,依赖变量通过一个有限系列近似表示,其中假设解的“形状”已知,并且取决于有限数量需要确定的参数。将伽辽金近似代入主导微分方程,产生的残差函数与权重函数相乘,要求在积分意义上与权重函数正交,即 \[\int W(x)R(T,x)dx=0\] 其中\(R(T, x)\)是残差函数(当将近似精确解\(T^*\)代入微分方程时得到的函数),\(W(x)\)是权重函数。从这些表达式中生成的一组线性代数方程允许我们确定未知参数,从而得到解的近似值。通过使用积分换元法降低二阶导数项,我们得到了“弱形式”公式。应用弱形式公式产生了一个通用的算法,可扩展到广泛的问题类别。